ABSTRACT. We prove new estimates for the volume of a Lorentzian manifold and show especially that cosmological spacetimes with crushing singularities have finite volume.
Date: April 18, 2002.
2000 Mathematics Subject Classification. 35J60, 53C21, 53C44, 53C50, 58J05.
Key words and phrases. Lorentzian manifold, volume estimates, cosmological spacetime, general relativity, constant mean curvature, CMC hypersurface.
Let N be a (n + 1)-dimensional Lorentzian manifold and suppose that N can be decomposed in the form
where N0 has finite volume and N- resp. N+ represent the critical past resp. future Cauchy developments with not necessarily a priori bounded volume. We assume that N+ is the future Cauchy development of a Cauchy hypersurface M1, and N- the past Cauchy development of a hypersurface M2, or, more precisely, we assume the existence of a time function x0, such that
and that the Lorentz metric can be expressed as
where x = (xi) are local coordinates for the space-like hypersurface M 1 if N+ is considered resp. M2 in case of N-.
The coordinate system (x
)
0<<n is supposed to be future directed,
i.e. the past directed unit normal (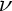
) of the level sets
is of the form
If we assume the mean curvature of the slices M(t) with respect to the past directed normal--cf. [4] for a more detailed explanation of our conventions--is strictly bounded away from zero, then, the following volume estimates can be proved
Theorem 0.1. Suppose there exists a positive constan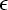t 
0 such
that
then
These estimates also hold locally, i.e. if Ei 
M(ti), i = 1, 2, are
measurable subsets and E1+,E
2- the corresponding future resp. past
directed cylinders, then,
and
In the following we shall only prove the estimate for N+, since the other case N- can easily be considered as a future development by reversing the time direction.
Let x = x(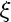
) be an embedding of a space-like hypersurface
and (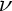) be the past directed normal. Then, we have the Gauß
formula
where (hij) is the second fundamental form, and the Weingarten equation
We emphasize that covariant derivatives, indicated simply by indices, are always full tensors.
The slices M(t) can be viewed as special embeddings of the form
where (xi) are coordinates of the initial slice M(t 1). Hence, the slices M(t) can be considered as the solution of the evolution problem
with initial hypersurface M(t1), in view of ( 0.5).
From the equation ( 1.4) we can immediately derive evolution
equations for the geometric quantities gij,hij,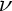, and H = gijh
ij of
M(t), cf. e.g. [3, Section 4], where the corresponding evolution
equations are derived in Riemannian space.
For our purpose, we are only interested in the evolution equation for the metric, and we deduce
in view of the Weingarten equation.
Let g = det(gij), then,
and thus, the volume of M(t),|M(t)|, evolves according to
where we shall assume without loss of generality that |M(t1| is finite, otherwise, we replace M(t1) by an arbitrary measurable subset of M(t1) with finite volume.
Now, let T 
[t1,T+) be arbitrary and denote by Q(t1,T) the
cylinder
then,
where we omit the volume elements, and where, M = M(x0).
By assumption, the mean curvature H of the slices is bounded
from below by 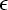0, and we conclude further, with the help of
( 1.7),
Letting T tend to T+ gives the estimate for |N+|.
To prove the estimate ( 0.10), we simply replace M(t1) by E1.
If we relax the conditions ( 0.6) and ( 0.7) to include the case 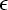0 = 0,
a volume estimate is still possible.
Theorem 1.1. If the assumptions of Theorem 0.1 are valid with
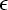0 = 0, and if in addition the length of any future directed curve
starting from M(t1) is bounded by a constant 
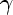1 and the length of any
past directed curve starting from M(t2) is bounded by a constant 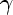2,
then,
Proof. As before, we only consider the estimate for N+.
From ( 1.6) we infer that the volume element of the slices M(t) is decreasing in t, and hence,
Furthermore, for fixed x M(t1) and t > t1
because the left-hand side is the length of the future directed curve
Let us now look at the cylinder Q(t1,T) as in ( 1.8) and ( 1.9). We have
by applying Fubini’s theorem and the estimates ( 1.13) and ( 1.14).
![[]](msam10-c-3.gif)
A cosmological spacetime is a globally hyperbolic Lorentzian manifold N with compact Cauchy hypersurface S0, that satisfies the timelike convergence condition, i.e.
If there exist crushing singularities, see [1] or [2] for a definition,
then, we proved in [2] that N can be foliated by spacelike hypersurfaces
M(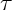
) of constant mean curvature , -
< < ,
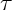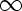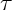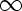where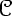 
0 consists either of a single maximal slice or of a whole
continuum of maximal slices in which case the metric is stationary in
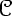0. But in any case 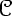0 is a compact subset of N.
In the complement of 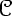0 the mean curvature function 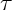is a regular
function with non-vanishing gradient that can be used as a new time
function, cf. [4] for a simple proof.
Thus, the Lorentz metric can be expressed in Gaussian coordinates
(x) with x0 = 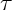as in ( 0.3). We choose arbitrary
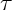2 < 0 < 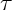1 and
define
Then, N0 is compact, and the volumes of N-,N+ can be estimated by
Hence, we have proved
Remark 2.2. Let N be a spacetime with compact Cauchy
hypersurface and suppose that a subset N- N is foliated by
constant mean curvature slices M(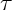) such that
and suppose furthermore, that x0 = 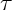is a time function--which will be
the case if the timelike convergence condition is satisfied--so that the
metric can be represented in Gaussian coordinates (x) with
x0 = .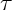
Consider the cylinder Q(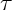,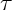2) = { 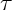< x0 <
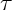2} for some fixed .
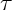Then,
and we obtain in view of ( 1.7)
and conclude further
i.e.
Suppose that N is a Riemannian manifold that is decomposed as in ( 0.1) with metric
The Gauß formula and the Weingarten equation for a hypersurface now have the form
As default normal vector--if such a choice is possible--we choose the outward normal, which, in case of the coordinate slices M(t) = {x0 = t} is given by
Thus, the coordinate slices are solutions of the evolution problem
and, therefore,
i.e. we have the opposite sign compared to the Lorentzian case leading to
The arguments in Section 1 now yield
Theorem 3.1. (i) Suppose there exists a positive constant 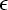0 such
that the mean curvature H(t) of the slices M(t) is estimated by
then
(ii) On the other hand, if the mean curvature H is negative in N+ and positive in N-, then, we obtain the same estimates as Theorem 0.1, namely,
[1] D. Eardley & L. Smarr, Time functions in numerical relativity: marginally bound dust collapse, Phys. Rev. D 19 (1979) 2239-2259.
[2] C. Gerhardt, H-surfaces in Lorentzian manifolds, Commun. Math. Phys. 89 (1983) 523-553.
[3] _________ , Hypersurfaces of prescribed Weingarten curvature, Math. Z. 224 (1997) 167-194. gerhardt/preprints
[4] _________ , On the foliation of space-time by constant mean curvature hypersurfaces, e-print, 7 pages, math.DG/0304423
[5] _________ , Hypersurfaces of prescribed curvature in Lorentzian manifolds, Indiana Univ. Math. J. 49 (2000) 1125-1153. gerhardt/preprints
[6] S. W. Hawking & G. F. R. Ellis, The large scale structure of space-time, Cambridge University Press, Cambridge, 1973.
RUPRECHT-KARLS-UNIVERSITÄT, INSTITUT FÜR ANGEWANDTE MATHEMATIK, IM NEUENHEIMER FELD 294, 69120 HEIDELBERG, GERMANY
E-mail address: gerhardt@math.uni-heidelberg.de
![-1
N+ = x0 ([t1,T+)), M1 = {x0 = t1},
(0.2) 0-1 0
N - = x ((T-,t2]), M2 = {x = t2},](LM-Volume-manuscript1x.gif)
